MSM Estimation

In this notebook we gonna show, how to estimate a transfer operator, namely a transition matrix from an already discretized trajectory.

##########################################
# IMPORT ALL REQUIRED PACKAGES
##########################################
# numerics
import numpy as np
# matplotlib
import matplotlib.pyplot as plt
%pylab inline
#emma imports
import pyemma.msm.io as msmio
import pyemma.msm.estimation as msmest
import pyemma.msm.analysis as msmana
import pyemma.msm.generation as msmgen

Populating the interactive namespace from numpy and matplotlib

IO

We first read a discrete trajectory that has been generated by clustering a TICA-projection of the 1 ms Anton BPTI trajectory:

dtraj_bpti = msmio.read_dtraj("./resources/bpti_tica2_regspace0.3.disctraj")
print len(dtraj_bpti)
print dtraj_bpti[0:20]

4124963
[0 2 2 3 4 2 0 2 7 1 0 7 6 0 1 3 3 1 2 2]

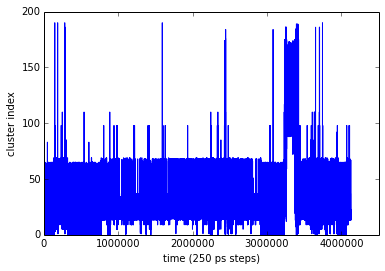
Although this is just a series of cluster indexes, let’s have a look at the trajectory in a plot. It’s pretty clear that there is something interested happening in the last third of the trajectory:

plot(range(len(dtraj_bpti)), dtraj_bpti)
xticks(range(0,len(dtraj_bpti),1000000))
xlabel('time (250 ps steps) ')
ylabel('cluster index')
show()

Trajectory generation

Now we want to generate our own trajectory data. For starters, consider the following simple 4x4 matrix which exhibits dynamics on three different timescales:

T4 = np.array([[0.9, 0.1,  0.0,  0.0],
             [0.1, 0.89, 0.01, 0.0],
             [0.0, 0.01, 0.94, 0.05],
             [0.0, 0.0,  0.05, 0.95]])

This matrix is stochastic (it’s a transition matrix) - see:

# test function
print "T is a transition matrix: ", msmana.is_transition_matrix(T4)
# proof that this is true:
print "because all its row sums are 1: ", np.sum(T4, axis=1)
print "and all its elements are within: [", np.min(T4), ",", np.max(T4), "]"

T is a transition matrix:  True
because all its row sums are 1:  [ 1.  1.  1.  1.]
and all its elements are within: [ 0.0 , 0.95 ]

Its stationary distribution is uniform:

mu = msmana.statdist(T4)
print "Stationary distribution:", mu

Stationary distribution: [ 0.25  0.25  0.25  0.25]

It’s also reverisble matrix:

# test function
print "T is a reversible matrix: ", msmana.is_reversible(T4)
# proof that this is true:
C = np.dot(np.diag(mu),T4)
print "because its correlation matrix \n", C
print "is symmetric to within numerical error of ", np.linalg.norm(C - C.transpose())

T is a reversible matrix:  True
because its correlation matrix
[[ 0.225   0.025   0.      0.    ]
 [ 0.025   0.2225  0.0025  0.    ]
 [ 0.      0.0025  0.235   0.0125]
 [ 0.      0.      0.0125  0.2375]]
is symmetric to within numerical error of  2.26512642969e-17

Buhuuuu! This is wrong.

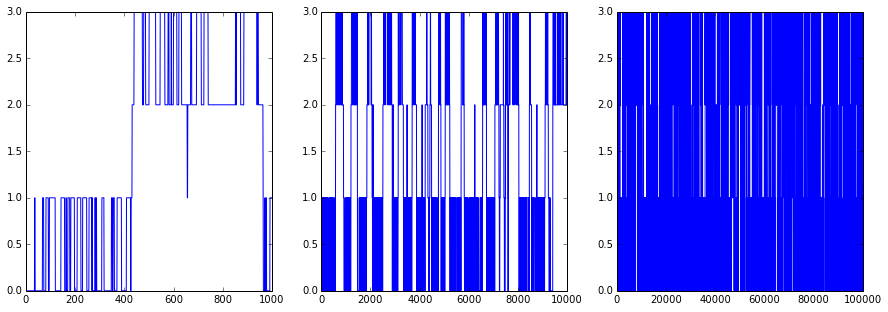
OK... Now we generate a trajectory from it:

figsize(15,5)
dtraj_4_1K = msmgen.generate_traj(T4, 0, 1000)
subplot2grid((1,3),(0,0))
plot(range(len(dtraj_4_1K)), dtraj_4_1K)
dtraj_4_10K = msmgen.generate_traj(T4, 0, 10000)
subplot2grid((1,3),(0,1))
plot(range(len(dtraj_4_10K)), dtraj_4_10K)
dtraj_4_100K = msmgen.generate_traj(T4, 0, 100000)
subplot2grid((1,3),(0,2))
plot(range(len(dtraj_4_100K)), dtraj_4_100K)
show()

Estimation

First of all we have to count

C = msmest.cmatrix(dtraj_4_10K, 1)
print C

(0, 0)    2655.0
(0, 1)    281.0
(1, 0)    280.0
(1, 1)    2730.0
(1, 2)    26.0
(2, 1)    25.0
(2, 2)    2067.0
(2, 3)    93.0
(3, 2)    92.0
(3, 3)    1750.0

Mind that this count matrix is now a sparse matrix! At the moment count matrices are sparse whereas subsequent operations (estimation, analysis) will work on either sparse or dense matrices, depending on the input matrix (although not all combinations are implemented yet).

This may be changed in the future because for small matrices, dense is the most efficient option.

Next, we estimate the transition matrix - either reversible or nonreversibly:

Test_nonrev = msmest.transition_matrix(C)
print Test_nonrev.toarray()
print
Test_rev = msmest.transition_matrix(C,reversible=True)
print Test_rev.toarray()
print

[[ 0.90429155  0.09570845  0.          0.        ]
 [ 0.09222661  0.89920949  0.0085639   0.        ]
 [ 0.          0.01144165  0.94599542  0.04256293]
 [ 0.          0.          0.04994571  0.95005429]]

[[ 0.90429155  0.09570845  0.          0.        ]
 [ 0.09222661  0.89920949  0.0085639   0.        ]
 [ 0.          0.01144165  0.94599542  0.04256293]
 [ 0.          0.          0.04994571  0.95005429]]

As you can see the results are almost identical (the differences are due to numerical reasons). This is because any tridiagonal transition matrix is reversible with respect to its stationary distribution - but we will see differences later.

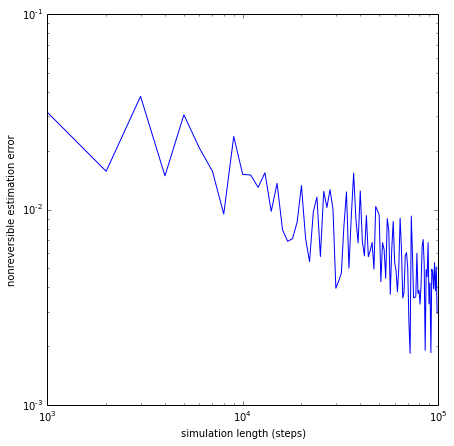
We now show that the estimate converges to the correct matrix for long sampling:

lengths = range(1000, 100000, 1000)
errors_nonrev = []
for l in lengths:
    dtraj_4_var = msmgen.generate_traj(T4, 0, l)
    Cest_4_var = msmest.count_matrix(dtraj_4_var, 1)
    Test_4_var = msmest.transition_matrix(Cest_4_var)
    error_nonrev = np.linalg.norm(Test_4_var - T4)
    errors_nonrev.append(error_nonrev)
# do a log-log plot of the error
figsize(7,7)
loglog(lengths, errors_nonrev)
xlabel('simulation length (steps)')
ylabel('nonreversible estimation error')
show()

Implied timescales

Now we conduct the implied timescales test using the BPTI trajectory. There’ll be a few high-level commands (certainly for the shell, maybe for the python API level as well) later, but right now you build things like implied timescales yourselves:

lags = [1,2,5,10,20,50,100,200,500,1000,2000,5000,10000]
nits = 10
evs = np.zeros((len(lags),nits))
its = np.zeros((len(lags),nits))
for i in range(len(lags)):
    lag = lags[i]
    # count matrix at lag tau
    Clag_sparse = msmest.cmatrix(dtraj_bpti,lag)
    # let's stay dense
    Clag = Clag_sparse.toarray()
    # estimate transition matrix
    Tlag = msmest.transition_matrix(Clag, lag)
    # eigenvalues
    evs[i,:] = msmana.eigenvalues(Tlag)[1:nits+1]
    # timescales
    its[i,:] = msmana.timescales(Tlag, lag)[1:nits+1]

-c:14: ComplexWarning: Casting complex values to real discards the imaginary part

Let’s have a look at the first eigenvalue and timescale

# plot eigenvalue
figsize(10,5)
subplot2grid((1,2),(0,0))
plot(lags, evs[:,0])
xlabel('lag time')
ylabel('eigenvalue')
# plot its
figsize(10,5)
subplot2grid((1,2),(0,1))
plot(lags, its[:,0])
xlabel('lag time')
ylabel('timescale')
show()

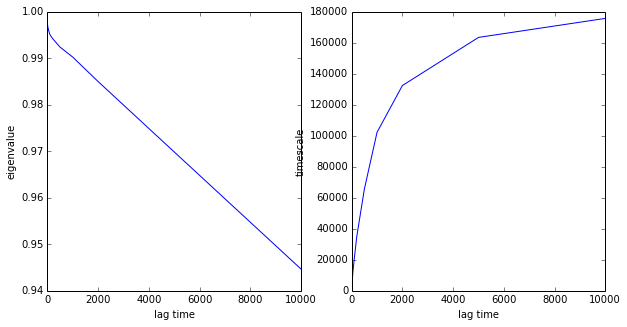
You can nicely see the problem with this kind of MSM estimation: the eigenvalue does not decay exponentially for all tau, but rather drops (due to fast processes that are not resolved by the discretization) to some value smaller than 1, and then decays exponentially with the timescale of interest. Hence we have slow convergence in tau.

Let’s look at all timescales

# plot its
figsize(10,5)
subplot2grid((1,2),(0,0))
for i in range(nits):
    plot(lags, its[:,i])
# plot forbidden region
plot(lags,lags,color='black', linewidth=3)
xlabel('lag time')
ylabel('timescale')
# logarithmically
figsize(10,5)
subplot2grid((1,2),(0,1))
for i in range(nits):
    plot(lags, its[:,i])
# plot forbidden region
plot(lags,lags,color='black', linewidth=3)
semilogy()
ylim(100,1000000)
xlabel('lag time')
ylabel('timescale')
show()

Example: Double-well potential

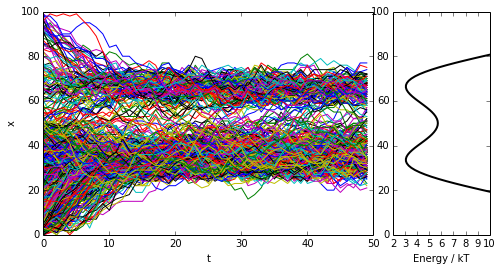
Next we probe a more complex quasi-continuous example: a metastable double-well potential with 100 microstates, out of which about 60 are populated with significant probability. We coarse-grain the double-well to a few (2 or more) sets. In the coarse-grained state space is usually connected.

# load T matrix
T_doublewell = msmio.read_matrix('./resources/2well.T',mode='sparse')
pi_doublewell = msmana.statdist(T_doublewell.toarray())
U_doublewell = -np.log(pi_doublewell)

trajs = []
for i in range(500):
    trajs.append(msmgen.generate_traj(T_doublewell.toarray(), random.randint(0,50), 500, dt=10))
for i in range(100):
    trajs.append(msmgen.generate_traj(T_doublewell.toarray(), random.randint(50,100), 500, dt=10))

figure(figsize=(8,4))
subplot2grid((1,4),(0,0),colspan=3)
for traj in trajs:
    plot(range(len(traj)), traj)
plt.xlabel('t')
plt.ylabel('x')
subplot2grid((1,4),(0,3))
plot(U_doublewell,range(len(U_doublewell)), linewidth=2, color='black')
xlim([2,10])
plt.xlabel('Energy / kT')
show()

# define discretization
def discretize(_trajs, _bounds):
    """discretizes the trajectories into two states split at point p"""
    _dtrajs = []
    for _traj in _trajs:
        _dtraj = np.digitize(_traj,_bounds)
        _dtrajs.append(_dtraj)
    return _dtrajs

# DECENT DISCRETIZATION
def its_doublewell(lags,discretization):
    dtrajs_1 = discretize(trajs,discretization)
    nits = len(discretization)
    its = np.zeros((len(lags),nits))
    for i in range(len(lags)):
        lag = lags[i]
        # count matrix
        Z = msmest.cmatrix(dtrajs_1, lag)
        # densify!
        Z = Z.toarray()
        # estimate
        T = msmest.transition_matrix(Z, reversible=True)
        # timescales
        its[i,:] = msmana.timescales(T, lag)[1:nits+1]
    return its

# DECENT discretization
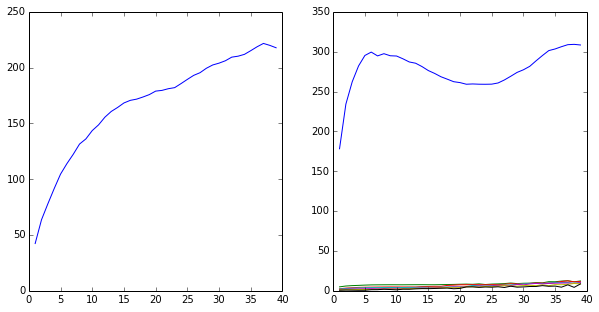
lags = range(1,40)
its2 = its_doublewell(lags,[50])
# GREAT discretization
lags = range(1,40)
its8 = its_doublewell(lags,[30,40,45,50,55,60,70])

subplot2grid((1,2),(0,0))
plot(lags,its2)
subplot2grid((1,2),(0,1))
plot(lags,its8)
show()

# ANALYZE ERRORS!!!!

Next - analyze errors, uncertainties