Transition path analysis for alanine-dipeptide

This notebook shows usage examples for transition path-analysis using the tpt (transition path theory) members of the emma.msm.analysis package.

A given MSM, estimated from alanine-dipeptide simulation data at lagtime \(\tau=6ps\), is used as an example to carry out analysis.

The necessary inputs are:

1. the transition matrix, ‘T.dat’
2. the centers of the \((\phi, \psi)\) dihedral angle space regular grid discretization, ‘grid_centers20x20.dat’
3. the largest set of connected microstates, ‘lcc.dat’

%pylab inline

from pyemma.msm.io import read_matrix

import plotting
import util

import matplotlib.pyplot as plt
import numpy as np
import itertools as it

Populating the interactive namespace from numpy and matplotlib

import the TPT functionality from emma. On API-level we provide shortcuts for

from pyemma.msm.analysis import tpt # this is the API function, creating the multi-purpose TPT object instance
from pyemma.msm.analysis import tpt_flux, tpt_netflux, tpt_rate, tpt_totalflux # these are shortcuts, for quick
from pyemma.msm.analysis.dense.tpt import TPT # the impl of the TPT class

import the committor functionality

from pyemma.msm.analysis import committor

Read the already created Markov model for alanine dipeptide

# load data
T = read_matrix('T.dat')
T.shape

(251, 251)

Read the the largest connected set and the cluster centers. Choose only those cluster centers, which are connected. - describe mapping

lcc = read_matrix('lcc.dat', dtype=int)
centers = read_matrix('grid_centers20x20.dat')[lcc , :]
lccmap=util.MapToConnectedStateLabels(lcc)

Metastable sets

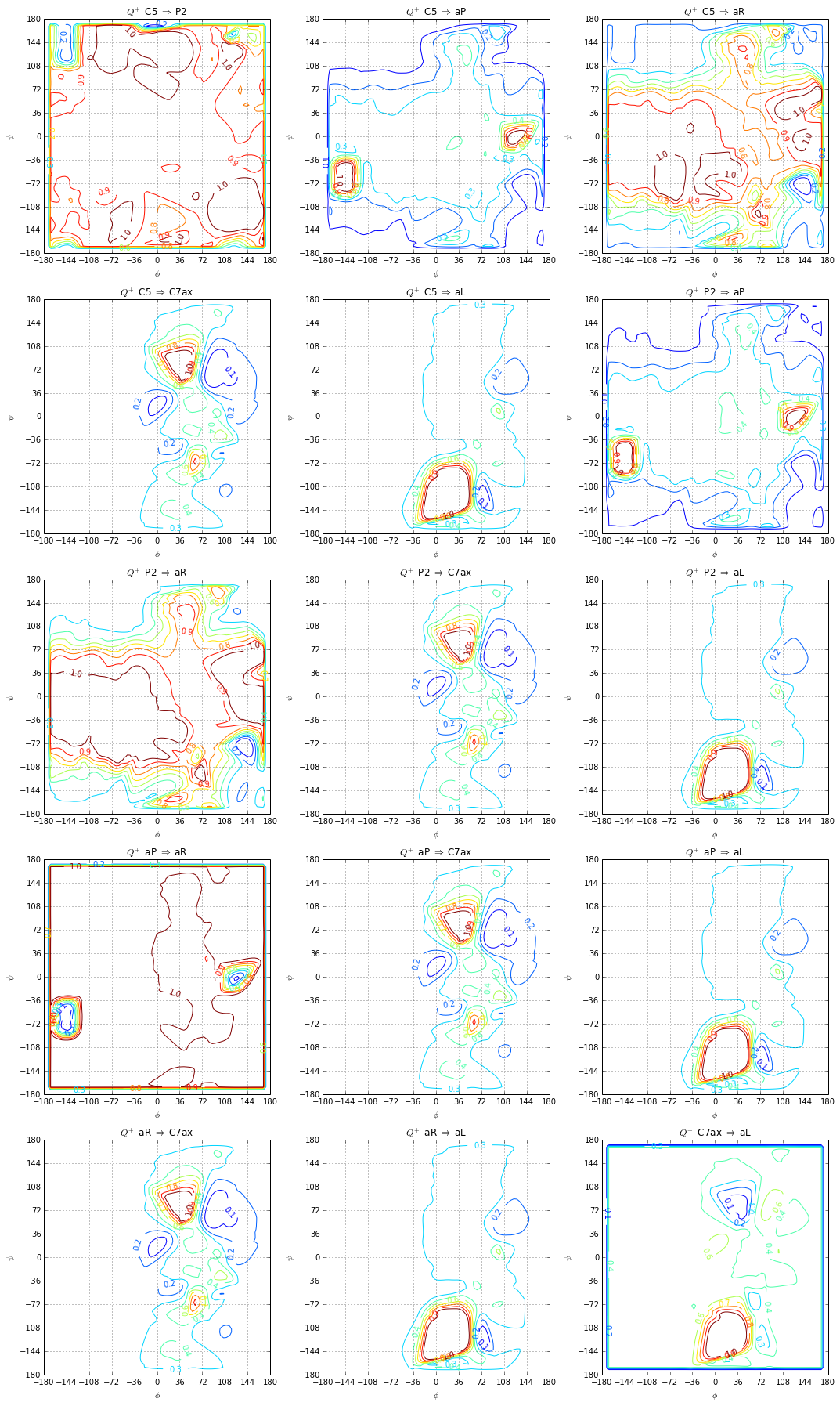
The two metastable sets \(C_5\) and \(C_7^{ax}\) in the dihedral angle plane are used to carry out the fingerprint analysis.

The \(C_5\)-conformation can be found with high probability in equilibrium while the \(C_7^{ax}\) conformation is only rarely visited.

C5 = [20, 40, 36, 37, 38, 39, 56, 57, 58, 59]
C7ax = [253, 254]


C5_mapped = lccmap.map(C5)
C7ax_mapped = lccmap.map(C7ax)

First we calculate the committors from the \(C_5\) to the \(C_7^{ax}\) set.

u = committor(T, C5_mapped, C7ax_mapped)
w = committor(T, C5_mapped, C7ax_mapped, forward=False) # Backward committor

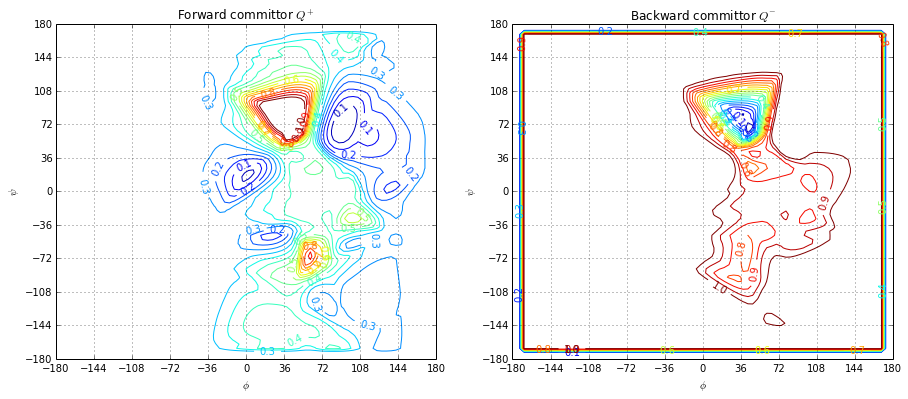
Because a direct plot of the committor would not respect our grid centers, we project the calculated values back into the \((\phi, \psi)\) dihedral angle space. This is implemented in the plotting module, which lies next to this notebook.

fig, axes = plt.subplots(ncols=3, figsize=(15,5))
fig.suptitle("$Q^+$: %s $ \Rightarrow $ %s" % ('$C_5$', '$C_7^{ax}$'), fontsize=16)
ax = axes[0]

ax.plot(u)
ax.set_xlabel('state')
ax.set_ylabel('P')

ax = axes[1]
ax.text(0, 0, "$\Rightarrow$", {'fontsize': 50})
ax.axis('scaled')
ax.axis('off')

plotting.committor(centers, u, levels=np.linspace(0.0, 1.0, 10), ax=axes[2])

plt.show()

Plot forward and backward committor

fig, ax = plt.subplots(1, 2, figsize=(15, 6))

ax[0].set_title("Forward committor $Q^+$")
ax[1].set_title("Backward committor $Q^-$")
ax[0].grid()
ax[1].grid()
plotting.committor(centers, u, levels=np.linspace(0.0, 1.0, 20), ax=ax[0])
plotting.committor(centers, w, levels=np.linspace(0.0, 1.0, 20), ax=ax[1])

plt.show()

Now we can use the committors for the TPT calculation. NOTE: this is optional, if they are not given, they will be calculated in the TPT class on initialization. You may also give the stationary distribution, if you have already calculated it.

tpt_c5_c7ax = TPT(T, C5_mapped, C7ax_mapped, qminus=w, qplus=u)
assert tpt_c5_c7ax.qminus is w
assert tpt_c5_c7ax.qplus is u

# access some quantities of the TPT object
print "Total flux:", tpt_c5_c7ax.totalflux
print "Rate:", tpt_c5_c7ax.rate

# show equivalence of both ways to calculate
assert np.all(tpt_flux(T, C5_mapped, C7ax_mapped,
                       mu=tpt_c5_c7ax.mu, qminus=w, qplus=u) == tpt_c5_c7ax.flux)

Total flux: 1.43589402556e-05
Rate: 1.43694776475e-05

Easy computation of transition paths between sets

Now we gonna define some other meta stable sets for Alanine-dipeptide and show how to easily pairwise calculate all quantaties on those pairs. We gonna use itertools to iterate over all pairwise combinations and also combine the names of the sets for easy plot title generation.

P2 = [116, 117, 118, 119, 136, 137, 138, 139]
aP = [25, 26, 27, 45, 46, 47]
aR = [105, 106, 107, 125, 126, 127]
aL = [242, 244]

metastableSets = [C5, P2, aP, aR, C7ax, aL]
names = ['C5', 'P2', 'aP', 'aR', 'C7ax', 'aL']

# apply map function to map microstates to connected microstates
X = map(lccmap.map, metastableSets)
# combine set names with their values
X_named = zip(names, X)

# calculate all pairs, without repeations
paths = []

for c in it.combinations(X_named, 2):
    print "calc tpt from %s to %s" % (c[0][0], c[1][0])
    paths.append(TPT(T, A=c[0][1], B=c[1][1], name_A=c[0][0], name_B=c[1][0]))

calc tpt from C5 to P2
calc tpt from C5 to aP
calc tpt from C5 to aR
calc tpt from C5 to C7ax
calc tpt from C5 to aL
calc tpt from P2 to aP
calc tpt from P2 to aR
calc tpt from P2 to C7ax
calc tpt from P2 to aL
calc tpt from aP to aR
calc tpt from aP to C7ax
calc tpt from aP to aL
calc tpt from aR to C7ax
calc tpt from aR to aL
calc tpt from C7ax to aL

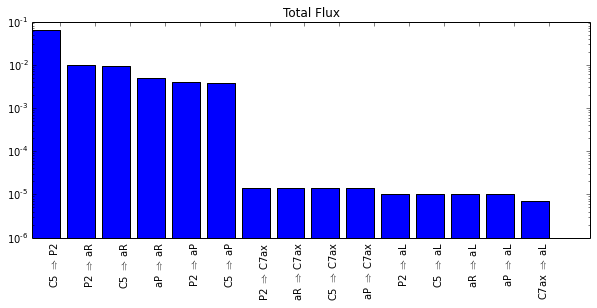
fig = figure(figsize=(10,5))
title("Total Flux")
inds = range(len(paths))
labels = []
fluxes = []
# sort tpt objects by total fluxes
paths_sorted_by_flux = sorted(paths, key=lambda t: t.totalflux, reverse=True)

for t in paths_sorted_by_flux:
    labels.append("%s $\Rightarrow$ %s" % (t.name_A, t.name_B))
    fluxes.append(t.totalflux)

h = plt.bar(inds, fluxes, label=labels, log=True)
plt.subplots_adjust(bottom=0.3)
xticks_pos = [patch.get_width() + patch.get_xy()[0] for patch in h]
plt.xticks(xticks_pos, labels,  ha='right', rotation=90)
plt.show()

fig, axes = plt.subplots(nrows=5, ncols=3, figsize=(15, 25))

for t, a in it.izip(paths, axes.flat):
    committor = t.get_forward_committor()
    plotting.committor(centers, committor, levels=np.linspace(0.0, 1.0, 10), ax=a)
    a.set_title("$Q^+$ %s $\Rightarrow$ %s" % (t.name_A, t.name_B))
    a.grid()

plt.tight_layout()
plt.show()