Fingerprint analysis for alanine-dipeptide¶

This notebook demonstrates usage of MSM for the computation of fingerprints. Fingerprints allow to compare computer simulations to experimental studies.

A given MSM, estimated from alanine-dipeptide simulation data at lagtime \(\tau=6ps\), is used as an example to carry out analysis.

The necessary inputs are:

the transition matrix, ‘T.dat’
the centers of the \((\phi, \psi)\) dihedral angle space regular grid discretization, ‘grid_centers20x20.dat’
the largest set of connected microstates, ‘lcc.dat’

Auxiliary functions in ‘plotting.py’ are used to generate figures of the estimated quantities.

Use ipythons magic % commands to activate plotting within notebook cells¶

%matplotlib inline

Imports are ordered as¶

standard library imports
third party imports
local application/library specific imports

import numpy as np

from pyemma.msm.io import read_matrix

from pyemma.msm.analysis import stationary_distribution, fingerprint_relaxation

import plotting

import util

Load necessary input data¶

Use pyemma.msm.io.read_matrix function to read dense arrays from ascii files. The returned objects will be dense arrays (numpy.ndarray).

T=read_matrix('T.dat')

lcc=read_matrix('lcc.dat', dtype=int)

grid=read_matrix('grid_centers20x20.dat')

centers=grid[lcc, :]

Compute the stationary distribution

mu=stationary_distribution(T)

Metastable sets¶

The two metastable sets \(C_5\) and \(C_7^{ax}\) in the dihedral angle plane are used to carry out the fingerprint analysis.

The \(C_5\)-conformation can be found with high probability in equilibrium while the \(C_7^{ax}\) conformation is only rarely visited.

C5=[20, 40, 36, 37, 38, 39, 56, 57, 58, 59]

C7ax=[253, 254, 273, 252, 272, 251, 271]

Use an utility object to map the states in the above set definitions to the corresponding states in the largest connected component.

lccmap=util.MapToConnectedStateLabels(lcc)

C5map=lccmap.map(C5)
C7axmap=lccmap.map(C7ax)

Observables¶

Observable obs1 indicates the system being in conformation \(C_5\) while obs2 indicates the system to be in the \(C_7^{ax}\) conformation.

obs1=np.zeros(T.shape[0])
obs1[C5map]=1.0

obs2=np.zeros(T.shape[0])
obs2[C7axmap]=1.0

Initial distribution¶

The initial distribution \(p_0\) is concentrated on the \(C_7^{ax}\) conformation.

This distribution corresponds to an experiment in which the system has been driven out of equilibrium and is relaxing from the \(C_7^{ax}\) conformation.

p0=np.zeros(T.shape[0])
p0[C7axmap]=mu[C7axmap]/mu[C7axmap].sum()

Fingerprint relaxation¶

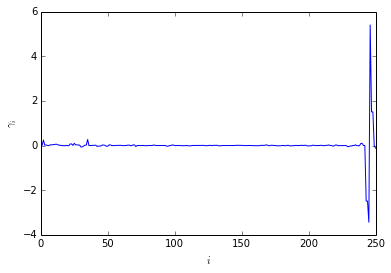
Compute fingerprint for obs1.

The fingerprint spectrum shows large amplitudes only for very fast processes. There is no slow process once the system reaches equilibrium and frequently visits the conformation \(C_5\).

ts, a=fingerprint_relaxation(T, p0, obs1)

/home/marscher/workspace/pyemma/emma2/msm/analysis/dense/decomposition.py:319: ImaginaryEigenValueWarning: Using eigenvalues with non-zero imaginary part for implied time scale computation
  'for implied time scale computation', ImaginaryEigenValueWarning)
/home/marscher/workspace/pyemma/emma2/msm/analysis/dense/fingerprints.py:97: ComplexWarning: Casting complex values to real discards the imaginary part
  amplitudes[i] = np.dot(p0, R[:,i]) * np.dot(L[i], obs)

plotting.amplitudes(a)

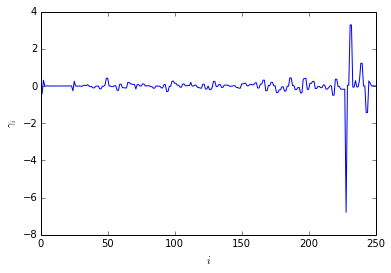
Compute fingerprint for obs2

The fingerprint shows large amplitudes for slow processes corresponding to the relaxation of the system from the initial non-equilibrium distribution \(p_0\) towards equilibrium.

The value of the observable decays with the second slowest time scale \(t_2\) in the long run. This due to the fact that most of the intial probability will be shifted to the high probaility conformations.

ts, a=fingerprint_relaxation(T, p0, obs2)

plotting.amplitudes(a)